admin – Erik C. Johnson

Leaky Integrate and Fire Neuron With Dynamic Threshold

A critical extension to the Leaky Integrate and Fire model is the addition of a dynamic threshold. In this model, the threshold changes with time, introducing critical properties such as spike frequency adaptation, relative refractoriness, and negative interspike interval correlations.

In the future, I hope to do a more thorough review of threshold models, but our first paper (2015) does a pretty decent job.

I’ve put together an implementation of a standard LIF model with dynamic threshold, following the work of Chacron, Longtin, and Maler in their 2001 paper “Negative interspike interval correlations increase the neuronal capacity for encoding time-dependent stimuli.” Not all the features of their model have been implemented in my code, but the critical dynamic threshold is there.

The model is here: https://bitbucket.org/erikjohnson24/eriksresearchcode/src/master/neural/lif_dt.m

And testing code: https://bitbucket.org/erikjohnson24/eriksresearchcode/src/master/neural/test_lif_dt.m

Simple Point Process Models of Neurons

In many parts of the nervous system, the spike times generated by neurons are quite random. For many experimental stimuli, repeated presentations results in randomly varied spike times. While this is definitely not always the case, as spike times can be quite reliable trial-to-trial, it is useful to have statistical models of spike trains as point processes.

The spike train model can be defined by its interspike intervals, $\Delta_i$ , which are the time between spikes. Different statistical models generate intervals from different distributions. Three common models (defined here in plain English, I hope) are

Poisson spike train- This approach models the spike train as a Poisson point processes. The intervals are identically, independently distributed with an exponential distribution defined by the rate parameter $\lambda$ in spikes per second. https://bitbucket.org/erikjohnson24/eriksresearchcode/src/master/neural/poisson_spikes.m
Renewal spike train- A general renewal point process also has identically, independently distributed intervals. To improve over the Poisson spike train, it makes sense to use the experimental interspike interval distribution to generate the intervals independently and identically. This will provide a match to the experimental data. https://bitbucket.org/erikjohnson24/eriksresearchcode/src/master/neural/renewal_spikes.m
Markov spike train- I originally came across these models in Dr. Ratnam and Dr. Nelson’s 2000 paper on anti-correlations in the spike trains of P-type afferents. This extends the renewal model by introducing a dependence on the previous interval. The next interval is then determined by the conditional distribution of interspike intervals given the previous interval. This can, of course, be extended to higher orders as well, although the code is only for the first order. This model can represent the statistical relationship between intervals, which are often observed experimentally. https://bitbucket.org/erikjohnson24/eriksresearchcode/src/master/neural/markov_spikes.m

Soon, I hope to get some code posted up on analyzing the statistics of spike trains, using these models as examples.

Comparing Spike Trains Using Coincidence

Git repository: https://bitbucket.org/erikjohnson24/eriksresearchcode

A problem that comes up again and again in neuroscience research is the comparison of spike-trains.

What is a spike-train? When looking at the membrane voltage along a neuron’s axon, you’ll see rapid depolarizations of the voltage termed action potentials or spikes. Neurons transmit sequences of spikes down their axons, called a spike-train. Since all the action potentials for a given neuron are (more or less) identical, such a signal can be represented as

$\sum_i \delta(t-t_i)$

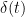where $\delta(t)$ is the Dirac delta function. In such a signal, information must be encoded in the time of the spikes.

How can one best compare two spike-trains? Someday I’d like to write up a full discussion of the problem, but here I’m just going to describe one metric, spike-time coincidence, and link some code.

Imagine two spike trains, with their rasters plotted below.

spikes

A raster plot of two simulated spike trains, one in blue, one in red. How similar are these two?

Are these similar? One intuitive idea is to see how often the spikes “line up”, and count the number of spikes which line up, or are coincident. This is the basic idea of the spike-time coincidence metric. Count up the number of spikes in the two spike trains which fall within a window of 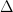$\Delta$ seconds of each other.

This is then normalized so that 1 corresponds to a perfect match between the two spike trains (the exact same number of spikes with all spikes coincident) and 0 corresponds to the expected number of coincidences for a Poisson process with similar spike-rate. The coincidence can go negative (a very bad match indeed). I believe this metric was introduced by Kistler, Gerstner, and Hemmen in 1997, modified from work by Joeken and Schwegler. Since then, it has been used quite a bit, notably in the INCF Spike-Time Prediction Competition (and less notably in the work from my lab).

The spike-time coincidence is defined as

$\Gamma = \frac{N_{\text{coin}}-E[N_{\text{coin}}]}{N_{\text{train}_1}+N_{\text{train}_2}} \frac{2}{1-2\nu \Delta}$

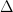where $\Delta$ is the coincidence window, $N_{\text{coin}}$ is the number of coincidences, $E[N_{\text{coin}}]$ is the number of expected coincidences from a Poisson point process with the same rate as the second spike-train, $N_{\text{train}_1}$ is the number of spikes in the first spike-train, $N_{\text{train}_2}$ is the number of spikes in the second spike-train, and $\nu$ is the spike rate of the second spike-train.

The key advantages of this metric are the intuition of counting which spikes “line up” and the fact that each spike time is taken into consideration. The only major assumption that has to be made is the window size 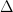$\Delta$ . This metric is a great way to compare spike-trains directly to say something like “X% of spikes were predicted with a Yms accuracy using our model.” The key downside, in my opinion, is the difficulty of mathematic analysis. The coincidence is nonlinear in the spike-times and has no particularly redeeming qualities from an optimization perspective.

Code to calculate coincidence is given here:

https://bitbucket.org/erikjohnson24/eriksresearchcode/src/master/neural/coin_calc.m

There is also testing code, where you can vary the jitter to see the change in coincidence.

Someday, I will hopefully find a time to do a more detailed comparison of spike-train metrics!

Leaky Integrate and Fire Neuron Discussion and Code

Git repository: https://bitbucket.org/erikjohnson24/eriksresearchcode

The Leaky Integrate and Fire (LIF) neuron is one of the most basic models of neural excitability and spiking. The LIF neuron is based on simplified electrical modeling of the semi-permeable membrane and lipid bilayer that is so fundamental to cells. Due to the selective ion channels embedded in the membrane, the cell maintains differing concentrations of charged ions in the extracellular and intracellular medium. This imbalance of ions results in a measurable membrane voltage, usually negative and in the 10s of millivolts.

Measurements and mathematical models of this voltage date back at least to Louis Lapicque, who studied its integrative properties. The integrative properties can be thought of as a capacitor circuit. Brunel and vanRossum have a nice historical discussion in “Lapicque’s 1907 paper: from frogs to integrate-and-fire”, which is well worth a read.

This was later extended to a resistor-capacitor circuit, known as an RC circuit. In the RC circuit, the capacitor provides an integrative component, building up voltage over time in response to a current input. The resistor, on the other hand, provides the ‘leak’ term, which limits the build up of voltage. In the signal processing world, this is a first-order low-pass analog filter. Ionic currents serve as the input to this filter and the output is the measured voltage.

Simple diagram of the RC circuit

This can be represented mathematically as

$\tau \frac{dv}{dt}=R I(t)- (V(t)-V_{\text{rest}})$

where $\tau$ is the time-constant and is equal to $RC$ , with units of seconds. $V_{\text{rest}}$ is the resting membrane potential of the cell, typically somewhere around -50 millivolts.

In this model, a positive step current will result in an exponential rise in voltage to a fixed level, and an exponential decay back to $V_{\text{rest}}$ when the step is finished.

The final piece needed to make this a spiking neuron model is to incorporate a threshold, $\theta$ . When

$V(t)=\theta$

a spike is fired and the voltage reset to $V_{\text{rest}}$ .

I’ve uploaded my matlab implementation of the LIF neuron to https://bitbucket.org/erikjohnson24/eriksresearchcode/src/master/neural/lif.m

This is specified as

function [voltage, spikes]=lif(current,threshold,tau,R,fs)

Where voltage is $V(t)$ and spikes is an array of the spike times. Current is the input current waveform, threshold is the threshold in millivolts. The variable $\tau$ is the time constant in seconds and $R$ the resistance in ohms. Finally, fs is the sampling frequency of the simulation.

Example usage is given in test_lif.m

Although the LIF is a simple model to analyze and explain, it fails to explain much observed neural activity. The predicted voltage is only loosely related to membrane voltages recorded experimentally (there is some relation to the subthreshold voltage, but that’s about it). The LIF is just the tip of the iceberg in neural modeling, but it provides a good starting place.